Resonance. No, it is not a Tesla-themed Evanescence cover band.
Resonance is a physics principle that, to be honest, most people will never need to know to go about their daily lives. So what is all the hubbub about resonance?
It is a word that is, even in the watch world, so mysterious and rare that it is heard only once or twice a decade (unless you’re specialized in such things).

Resonance wristwatch trio: Armin Strom Mirrored Force Resonance, Haldimann H2 Flying Resonance, and F.P. Journe Chronomètre à Résonance
As far as I am aware, there have only been three wristwatches ever developed featuring the fabled phenomenon of resonance: the F.P. Journe Chronomètre à Résonance, Beat Haldimann’s H2 Flying Resonance, and the recent Armin Strom Mirrored Force Resonance. There have been a handful of pocket watches and clocks as well, with the first ones showing up around 200 years ago.

Breguet N° 2667 resonance pocket watch from 1814
Resonance watches are special in that they use two balances that sync up through the resonance phenomenon, allowing them to keep a much more stable rate. Each helps the other to stay consistent and, due to resonance, offsets any variation from the other. This differs from watches with differentials, which use clever gear systems to balance out averages. But resonance literally changes the way each balance oscillates.
It seems a lot like magic unless you are well versed in the physics of energy transference.
Each one of the handful of existing timepieces approaches the phenomenon a little differently, but each one was created in the quest for better rate stability.
But that doesn’t tell you what it is, and many explanations available speak in often obscure copy/paste dictionary and Wikipedia definitions. In October 2017, we published a detailed horological breakdown of how resonance technically works in relation to the Armin Strom Mirrored Force Resonance by a watchmaker, but that only specifically related the details of this particular watch and mechanisms and not the phenomenon as a whole.
Here I explain in a hopefully easy-to-understand way what resonance is, the principles it is based on, why it works, and why resonance is rather remarkable and important in regards to chronometry.
Resonance by the book
The concept of resonance is rather basic, but employs very specific functions of physics to achieve a goal. The basic definition of resonance is “a phenomenon in which a vibrating system or external force drives another system to oscillate with greater amplitude at specific frequencies.”
Okay great, I get it. Well, not really.
First we have to realize that that is a general definition of resonance, and we are more concerned with the specific phenomenon called mechanical resonance, which is “the tendency of a mechanical system to respond at greater amplitude when the frequency of its oscillations matches the system’s natural frequency of vibration.”
Ahh, now it’s clear. Clear as mud.
These definitions don’t go very far to explain the phenomenon to anyone other than those currently studying math and physics or those who have a decent background in related topics. So let’s break it down from the basics.

Gold movement of the F.P. Journe Chronomètre à Résonance
Resonance: vibration and waves are the building blocks
The first critical thing to understand is that the resonance phenomenon strictly deals with the energy transfer from vibrations and their waves. You may know that vibrations can be shown in a wave form with high crests and low troughs. This depiction, which emulates how strings on a violin move, visualizes where the energy of a vibration is.
At each crest, the energy is highly potential as the oscillating wave reaches its highest point, stops momentarily, and then falls back toward the center point of the wave. In the center of the wave between the crest and the trough, the energy is highly kinetic as it is oscillating (we’ll cover the importance of that word later) from one extreme to the other.
Waves (and the vibrations they represent) have a very unique way of interacting with the physical universe. When two waves meet, like on the surface of a pond or sound waves in the air, they combine or interfere with each other.
How they interact depends on a variety of factors, but waves generally do one of four things: constructively interfere, destructively interfere, reflect, or result in linear superposition.
Destructive interference and linear superposition, while interesting, do not play a significant role in a resonance phenomenon as we are looking at it, so I will ignore them for this discussion.
The other two – constructive interference and reflection – are where the magic begins.
Resonance: constructive interference
Constructive interference happens to waves that have the same wavelength or frequency – in other words, the period between each pair of wave crests and troughs.
This is also called pitch, as in a sound pitch (frequency), and is the literal distance between two points of the same spot in a repeating pattern. This perfectly describes how waves in the ocean work; you can measure the crest of one wave to the crest of the next wave. That distance is the wavelength, and distance in relation to time is called frequency.
When two vibration waves have the same frequency and meet, the wave crests and troughs will either match, mirror each other, or something in between.
When they mirror each other, this causes destructive interference, meaning they cancel each other out. But when they match, they constructively interfere. This means that the energy of each point along the wave increases, so the crests and troughs grow larger, gaining higher amplitude.
This can be observed in ripples in a pond or two kids whipping each end of a jump rope, causing a wave to meet in the middle.
Pushing a child’s swing
But the best demonstration for our purposes is a child’s swing with someone pushing. If a swing is pushed once, it will swing back and forth, losing energy each time until it comes to rest, an example of a wave losing amplitude.
But if you push on that swing at precisely the right time, just like a “wave” of the same frequency meeting the “wave” of the swing, you can keep the swing going and even make it go higher. In that scenario, you are matching the frequency of the swing and constructively interfering with its wave (since its movement can be plotted as a wave).
Resonance was always there
The reason the example of the swing is applicable is because according to the definition of resonance, that is exactly how a balance and a hairspring oscillate at a consistent rate.
It has been stated before that all watches – and clocks, for that matter – work through the principle of resonance as the balance is just like the swing: it gets a push at just the right time to increase its amplitude to the resonant frequency of the system.
That’s actually all that resonance is: some external force or vibration acting upon a system, causing it to increasingly vibrate until it matches the resonant frequency of the mechanical system. Resonant frequency is the natural frequency at which an object or system vibrates most easily.
In this case the external force is the impulse jewel on the escapement lever exerting force on a balance wheel and hairspring assembly. The balance and hairspring is the “mechanical system” that has a resonant frequency, that usually being the frequency it was designed to oscillate at from 2.5 to 5 Hz.
The word “oscillate” is very important to this entire discussion. Energy moving back and forth, vibrating like the playground swing, is what resonance is all about. And it’s the oscillations that change when the resonance phenomenon comes into play.
But when we talk about resonance in the way of two balances keeping each other in a matched stable rate, the change in oscillation is actually due to the other fundamental way that waves interact mentioned above: reflection.
Reflection leads to stability
Now we come to the meat of the problem: two separate mechanical systems that vibrate at their resonant frequencies.

Armin Strom Mirrored Force Resonance
In the cases of F.P. Journe’s Chronomètre à Resonance and Armin Strom’s Mirrored Force Resonance, there are two completely separate gear trains leading to the twin oscillators with individual escapements.
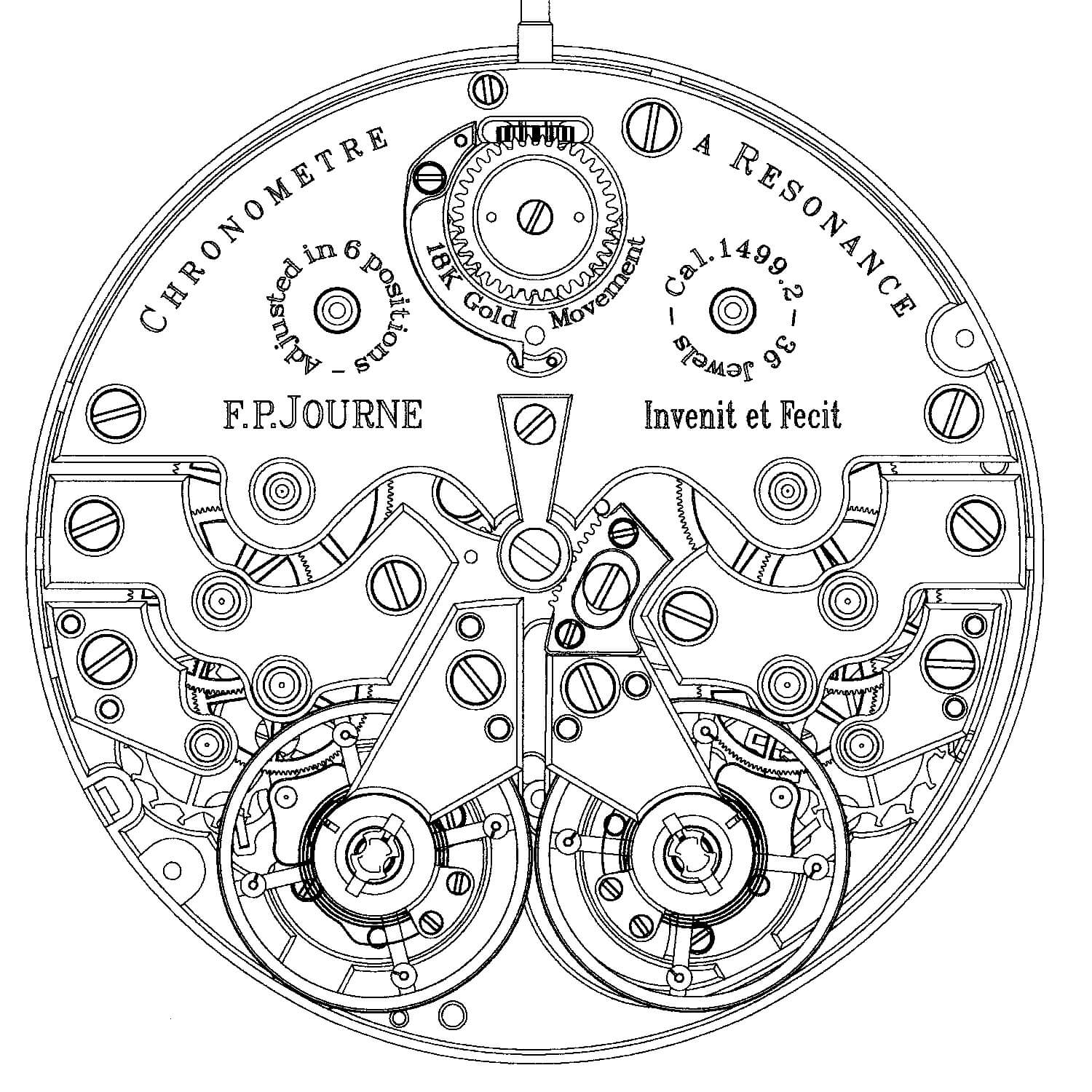
Movement diagram of the largely symmetrical F.P. Journe Chronomètre à Résonance
Haldimann’s H2 Flying Resonance has one gear train powering twin flying tourbillons rotating around a shared central axis. Each balance has its own escapement, meaning they are still separate resonant mechanical systems.

Beat Haldimann H2 Flying Resonance
Since both balances are operating through resonance, it isn’t the general concept of resonance that makes the true magic happen; it is how resonance affects other resonant systems via wave reflection.
Let’s break down how reflection affects vibration waves using the analogy of a long rope tied to a pole.
A child wiggles the end of the rope to vibrate it, creating a cresting wave (like we all did with that jump rope when we were kids). The wave travels down the rope before reaching the pole. When it reaches the pole at the end of the rope, held firm, it reflects the wave back along the rope, shifting a crest to a trough and putting the wave out of phase. This is an example of a single wave reflection.
Now, let’s imagine the same rope but with children on each end. These children represent the twin balance wheels on a resonance watch.
On the outward ends of the rope, two children “vibrate” each of the ends creating waves in the rope coming from each direction. If child A makes a large wave travel down the rope, and child B makes a small wave, the waves will pass in the middle (and momentarily constructively or destructively interfere) before continuing on to the opposite ends. The children each have waves coming toward them: a small wave toward child A and a large wave toward child B.
This is where the reflection happens. If each child holds the end of the rope still, they aren’t going to be thrown off their feet from the wave coming down the rope. But they will absorb a small amount of energy from the wave before reflecting it back to the other child. Now each wave is a bit smaller, having lost some energy to each child.
When we return from the rope analogy to the two balances in a resonance watch, each oscillation of the balances is the same as each child making a wave in the rope. Every time a balance wheel reaches its peak amplitude, it sends a small amount of energy as a vibration wave to the other balance and vice versa.
The wave reaches the other balance and is reflected back, but not before losing a bit of energy to that balance. That small amount of energy subtly shifts the balance wheel’s oscillation period, making it a bit different.
Why resonance works
Now it’s time for the magic.
Depending on how the balances are mechanically linked, the reflecting waves will do different things. Overall, the reflecting wave energy forces the balances to move on a very small scale, slightly changing the oscillating amplitude.
Each of the watches mentioned above uses a different method to achieve the same end result by slightly different energy transfers.
F.P. Journe Chronomètre à Résonance
In the F.P. Journe Chronomètre à Résonance, the two balances are mounted to the same main plate with two separate cocks and placed very close together. The proximity, combined with careful design of the main plate, allows the vibration waves to move through the rigid metal of the main plate and affect the oscillation of the other balance by slightly shifting its period. The energy is such a small value that the effect is extremely minimal.

F.P. Journe Chronomètre à Résonance
If both of the balances are not regulated to within five seconds per day of the same frequency in all positions (which in this case is 3 Hz), the difference in frequency and the amount of phase shift will be too great for the small amount of energy transfer to shift the two balances frequencies to be perfectly in phase. In fact, they are exactly 180 degrees out of phase, which has both balances rotating in opposite (mirrored) directions.
Also, the hairsprings must be free sprung as this adds rigidity to the mounting of the spring and therefore the energy transfer of the vibration into the balance cock. A spring attached to a regulator isolates the force too much and dissipates the wave before it can reach the other balance.
Haldimann H2
In the case of the Haldimann H2 Flying Resonance, the Journe method of reflected resonance would be impossible as the two balances are suspended and flying around on a tourbillon carriage.
The energy transfer needs to be completed in another way. The hairsprings on the two balances are also free sprung, but instead of springs mounted rigidly to a balance cock (not much of a structure on the twin flying tourbillon cage) they are attached to a “resonance coupling spring.” This spring is basically a somewhat stiff blade that spans the tourbillon cage with each hairspring mounted to it.

Beat Haldimann H2 Flying Resonance
The hairsprings both push on the coupling spring at the extents of each oscillation, sending a very short vibration wave across to the opposite balance. This transfer of energy is pretty direct and automatically adjusts the beat rate of the balance by changing the length of the hairspring ever so slightly.
Again, both balances need to be adjusted very precisely to within about five seconds per day of the same frequency (2.5 Hz) for the phase alignment to take place. But there is no worry about the energy being transferred as the hairsprings are tied together and not relying on vibrational energy passing through balance staff pivots, jewels, balance cocks, and main plates.
Armin Strom Mirrored Force Resonance
The Armin Strom Mirrored Force Resonance uses a similar concept as the Haldimann H2 but in a rather different way. The Armin Strom Mirrored Force Resonance uses two gear trains, like the F.P. Journe, but has them running in opposite directions. This ensures the two balances run 180 degrees out of phase as well, but in a way that creates more visual impact as the lower second hand runs in reverse.
But while it is set up similarly to the F.P. Journe in terms of gear trains, the Armin Strom actually borrows from the coupling spring idea and introduces its own “resonance clutch spring.” Unlike the Haldimann, the Armin Strom clutch spring is long, sinewy, and rigidly mounted on each end. The complex shape of the clutch spring has two locations for a floating hairspring stud about a third of the way from each end of the clutch spring.

Armin Strom Mirrored Force Resonance
The hairsprings mount to these studs, and through the gentle oscillation of the center portion of the clutch spring each balance sends a vibration wave with a small amount of energy to the other hairspring and balance until they begin to oscillate together 180 degrees out of phase.
But since the mounting points aren’t at the end of a floating spring, but instead in the middle of a rigidly mounted spring that is very specifically shaped, the deformation of the clutch spring moves almost perfectly linearly.
This is so the system has more control over the application of adjustment to the other hairspring; floating studs now act like constantly moving regulator arms. Once this happens, the entire clutch spring is actually oscillating itself, providing constant adjustment faster and slower during each oscillation to each balance.

Armin Strom Mirrored Force Resonance Fire
This setup has the very unique aspect of not requiring precise adjustment of each balance to be within five seconds per day; in fact the two balances could deviate by up to 250 seconds per day from each other and would still want to oscillate together. Of course, the balances are still adjusted very precisely, both beating at 3.5 Hz.
But the unique coupling method does mean slower resynchronization, taking a few minutes after a serious jolt and up to ten minutes to resynchronize when the power reserve runs out and you must wind it again.
Why resonance matters
Still, the resonance phenomenon, or perhaps more accurately reflected resonance, isn’t as much about precision as it is about consistency. In horology, precision is often touted as the ultimate goal of a fine watch, but in reality precision alone doesn’t make a great timekeeper: it’s consistency.
Consistency of rate is what actually makes your watch keep time perfectly over days, weeks, or months.
If a watch is expertly adjusted to within five seconds a day or, better yet, five seconds per week, that is remarkable precision. But if that same watch (assuming it is not on a watch timer being tested for accuracy) is subjected to shocks and temperature changes, resulting in drastic variations in overall rate, then it could easily gain or lose many seconds or minutes every day if worn in greatly differing circumstances.
If you have a watch that is adjusted to lose 30 seconds every day, but it only ever loses those 30 seconds, no more and no less, then that watch is much more reliable for accurate timekeeping as you can count on it being slow by 30 seconds every 24 hours. You can also adjust for that every day or two and maintain a watch that is very accurate over the long term.
This is what resonance seeks to accomplish. Along with mechanisms such as the remontoire d’égalité/constant force, tourbillon (in pocket watches), and dual balances with a differential, resonance watches seek to average out and reduce variations in rate to provide not more precise timekeeping, but more consistent timekeeping.
Consistency is much more valuable in the long run, and the resonance phenomenon uses physics to keep balances as stable in their rate as possible.
It also uses minute energy transfers that would normally be lost to friction, heat, or component wear and turns it into a restorative force.
Using vibrations to maintain a completely separate vibration is pretty genius, and the men that first understood the possibilities were basically wizards. Christiaan Huygens, Antide Janvier, Abraham-Louis Breguet, and the handful of clever horologists that have dabbled with physics most physicists don’t dabble in and structural engineers have nightmares about.
So while resonance might be a bit complicated when it comes to the math involved, the process is rather simple: have two things vibrate near each other and they will affect each other. Easy-peasy, right?
Well, judging by the fact that there are still only three production wristwatches to ever feature the phenomenon, I’m guessing it is still rather difficult. Hopefully, this long breakdown walked you through exactly why resonance is a pretty cool thing and why it is pretty rare in watches.
Compared to making a resonance watch, most horological feats might just be more of a walk in the park.
* This article was first published on December 17, 2017 at Understanding Resonance, Featuring The F.P. Journe Chronomètre à Résonance, Armin Strom Mirrored Force Resonance, And Haldimann H2 Flying Resonance.
You may also enjoy:
Armin Strom Masterpiece 1 Dual Time Resonance: Simplifying With Complexity
Leave a Reply
Want to join the discussion?Feel free to contribute!
















































Well thought out and written article, but since this is a scientific discussion you shouldn’t have mentioned the word ‘magic’ so much.
Thanks for the comment! I stand by my use of the words “magic” and “wizards” as they are literary devices meant to emphasize how incredible the physics is. If this were a scientific paper, the words might create confusion, but in this context I find it adds my own flavor to complex discussions. Also, I subscribe to Arthur C. Clarke’s third law that “Any sufficiently advanced technology is indistinguishable from magic,” which informs my passion for science and technology. I don’t think the text reads as if I am honestly saying it is magic, but instead is such a subtle influence that it could almost be believed to be magic (something that many scientific principles were believed to be at different times in history). But I will keep this in mind for future articles so that I do not accidentally create any confusion!
Very nice article.
Clocks were mentioned and indeed resonance can be used creatively in clocks, often with twin pendulums, and the BHI HQ has one with three.
However, resonance also explains the mysterious phenomenon of “Wednesday stopping”. People with week-running long case, or tall, clocks usually wind them on a Sunday. By Wednesday the driving weights are about level with the pendulum and if the case is free to rock, even imperceptibly, the pendulum support reaction will set up a counter oscillation which will stop the clock.
That is extremely interesting, Timothy, I was not aware of that! Definitely a perfect example of the resonance phenomenon playing an unwanted role in clocks outside of clockmakers’ intentions. Thank you for that addition!