Equation of Time (EoT): What is It and What’s the Attraction?
by Ashton Tracy
In its simplest form, the equation of time is defined as the difference between the time displayed by the position of the sun (as by a sundial) and the time displayed by any modern clock.
For centuries, watch- and clockmakers have utilized mechanisms indicating the equation of time to display the difference between a true solar day and a mean (average) solar day.
Mainly seen in complex astronomical clocks of the past, modern watchmakers makers sometimes feature an equation of time display on their highest-grade movements. Audemars Piguet, Breguet, Blancpain, and Panerai have all featured the equation of time complications, usually paired with a perpetual calendar.

Functions and indications of the George Daniels Space Travellers’ watch
One of my personal favorites equipped with this complication is The Space Traveller’s Watch by George Daniels, a handmade pocket watch that took ultra-complication to a stratospheric level.
————————————————————————————————————–
—————————————————————————————————–
What is a true solar day?
A true solar day (based on what astronomers call apparent solar time) is the length of time it takes for two consecutive passages of the sun to pass across a meridian at any given point; in other words, the length of time between two true noons (when the gnomon casts shortest shadow).

The gnomon projects from the lizard’s back on this sundial located on Agenhor’s grounds in Geneva
A true solar day cannot be trusted as a unit of time because the length of a day varies due to the earth having an elliptical orbit and because its axis is tilted. To combat this we use mean solar time, an average taken over all solar days, arriving at 24 hours.
What is a mean (average) solar day?
The very simplest explanation of a mean solar day is the even division into 24 segments of 60 minutes, which themselves are made up of 60 seconds each, by the gears of a watch or clock.
During the course of a year, there are four times when mean solar time and true solar time correspond, meaning both comprise nearly exactly 24 hours. Those points occur in the months of March, June, September, and December.
All other days throughout the year are either longer or shorter with a maximum difference of (approximately) minus 16 minutes in early November to plus 14 minutes in February, with various times in between.

View through the display back of the Greubel Forsey Quantième Perpétuel à Équation: the equation of time ‘manta ray’ and display is at 8 o’clock with the four-digit year beside it, while the back of the 25-degree inclined 24-second tourbillon can be seen under the polished bridge at 2 o’clock
—————————————————————————————————–
—————————————————————————————————–
A brief history of the equation of time
As far back as the fifth century AD, humans observed that solar time was inaccurate throughout the year when compared with measurement against another time-keeping device. Up to the sixteenth century, clocks were not generally accurate enough for this to be of any real concern, though.
In the mid-seventeenth century that all changed with the introduction of pendulums, better escapements, and watches equipped with balance springs. Timekeepers were now satisfactorily accurate to determine the exact difference between true and mean time at various stages throughout the year.
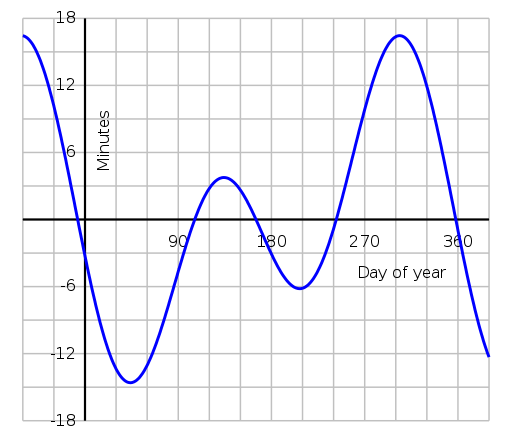
This graph of the equation of time shows how far our mean solar time deviates ahead of and behind true solar time
Printed tables were produced that accurately stated the difference between the two for every day of the year. Early longcase clocks were commonly sold with these equation tables, allowing the owner to calculate the difference.
Next came equation clocks, which displayed true and mean solar time without the need for calculations.
In the year 1719 a letter published in the Philosophical Transactions of The Royal Society, volume 30, states a claim made by Joseph Williamson, watchmaker, in which he “asserts his right to the curious and useful invention of making clocks keep time with the sun’s apparent motion.”
In his letter, Williamson expresses his outrage stemming from his reading of a French publication in which the author claimed to have been “making clocks that agree with the sun’s apparent motion; and suppose that it was a thing never thought of by any before himself.”
Williamson’s clock displayed true solar time on the dial by using a cam that adjusted the length of the pendulum throughout the year, depending on the difference between solar and mean time. Other notable makers of equation clocks include Thomas Tompion and Ferdinand Berthoud.
Due to the increase in accuracy of timekeeping, major cities around the world slowly began to adopt mean time as opposed to solar time as the standard in timekeeping: Geneva around 1780; England in 1792; and Berlin in 1810.
—————————————————————————————————–
—————————————————————————————————–
The current equation of time complication
To successfully track true solar time we must first track mean solar time; then the difference can be calculated and displayed.

Breguet Marine Équation Marchante Reference 5887 in platinum
In modern watches, this is accomplished in two ways. The first is via a subsidiary dial on the watch with a hand that indicates from minus 16 to plus 14 minutes. The subsidiary hand is driven by a kidney-shaped cam whose profile reflects the differences between mean and true solar time.
Throughout the year the difference between the two will vary, and the hand will point to the position on the dial indicating the current difference in minutes; the user must then perform the calculation.

The Martin Braun Eos Boreas was the first wristwatch to make the equation of time complication more accessible to a somewhat broader audience in a stainless steel case
The second way to do this is with a direct-reading “solar” minute hand mounted on a shaft concentric with the normal (mean) minute hand and using the same type of cam as before. The Breguet Reference 5887 pictured above is a good example of this.
The solar minute hand automatically tracks the time indicated by the sun on the same dial and in the same way as the normal minutes. In this instance, the calculation has already been solved and the “normal” dial is easy to read.
This does require a more complex mechanism behind the scenes, though, due to the extra wheels needed to display the time on the same axis. It’s worth noting that the precise (to fractions of a second rather than minutes) equation of time changes depending on the longitude of your location.
In today’s modern world most of us never need to think about the difference between true and mean solar time; however, like most things in twenty-first-century watchmaking necessity is not the goal; we do it because we can.
Modern watches that are considered ultra-complicated are occasionally still fitted with the equation of time complication. Here, it usually features together with a moon phase and perpetual calendar, tying in with the astronomical theme.
The equation of time complication is not particularly complicated to produce with today’s manufacturing techniques, and considering some of the latest advances in watchmaking it pales into the background.
What equation of time does do is hark back to a period of history I very much admire; a period of ingenuity and mechanical advancement, and one that we would be wise not to forget and to always respect.
* This article was first published on April 24, 2018 at Equation Of Time: What Is It And What’s The Attraction In A Watch?
You might also enjoy:
Breguet Marine Équation Marchante Reference 5887: Equating Time On The Run
Mechanical Computers From Then To Now: Greubel Forsey Quantième Perpétuel à Équation
De Fossard Solar Time Clock: Appreciating An Extreme Achievement Without A Loupe
Leave a Reply
Want to join the discussion?Feel free to contribute!






Thank you for the very interesting and informative article. I enjoyed reading it and seeing the beautiful implementations in watches.
But the following sentence caught my attention: “It’s worth noting that the equation of time changes depending on the latitude of your location, meaning watches displaying the equation of time need custom cams made for different areas of the world.” Could you verify if this is really the case?
I know there are other complications that are configured according to the owner’s home location latitude, but based on your explanation, it would seem that the equation of time is universal for all locations.
That’s an excellent question Petri and you have highlighted an error (now corrected) in the text: precise EoT depends on longitude on latitude.
My understanding is that watches displaying EoT are generally accurate (regarding EoT) to the minute and so do not require cams. However, if you wish to have EoT accurate to a fraction of a second then you need to take longitude into consideration.
From https://aa.usno.navy.mil/faq/eqtime
The Equation of Time is the difference between apparent solar time minus mean solar time. Apparent solar time is what a perfectly constructed and calibrated sundial would read at a given location; it is based on the actual position of the Sun in the sky. In astronomical terms, it is determined by the local hour angle of the true Sun, which is a measure of the Sun’s angular distance east or west of the local meridian (see box at right for definitions). Since each meridian is a line of constant longitude, apparent solar time is different for every longitude.
Mean solar time is different at every longitude. However, civil time is the same for all locations within a time zone. Therefore, civil time can be considered a good approximation to local mean solar time only along the defining meridian of longitude in each time zone, and only when daylight time (summer time) is not in effect. The longitudes of the defining meridians of the time zones, expressed in degrees, are evenly divisible by 15, and are usually near the center of their zone. For other places in the same time zone, mean solar time is 4 minutes earlier (later) than civil time for each degree of longitude east (west) of the defining meridian.
Regards, Ian
An interesting article but the reference to the brilliant Martin Braun’s EOS is missleading. It displayed not the Equation of Time but more usefully the times of Sunrise and Sunset, which (except at the Equator) vary with the season. They also vary with Longitude so Braun provided cams suitable for the owner’s location. From memory I think he made do with four sets. He was a really brilliant and genuinely innovative independent watchmaker. Such a pity he lost his business – but that’s another story…
Thanks for pointing that out Tim and I agree, Martin is an incredibly innovative watchmaker.
Regards, Ian
Tim it is you who is incorrect. The Eos Boreas displays EOT immediately beneath the date if you care to check. You are confusing this model with the standard EOS.